いまどき計算ですか?
生産部のHです。
組版の分野に携わって、数十年…たちました。
かつての電算写植では、級数表・歯送り表・電卓は必須の道具でした。版面サイズの指定をするだけでも「計算」が必要だったのです。

いまでは、「電算写植」というコトバさえ知らない世代が、主力として活躍していますね。
さて、DTPにおける組版ソフトでは、「版面サイズの計算」など出来なくても、殆ど支障はありません。面倒な計算はソフトウェアがやってくれます。
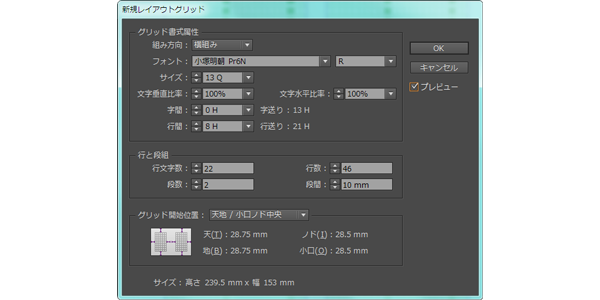
しかしながら、基本中の基本なので、「行長の計算」をあえてここに…
例1)13Q 字詰22倍 2段組 段間40Hの行長は、
13×22×2+40=612
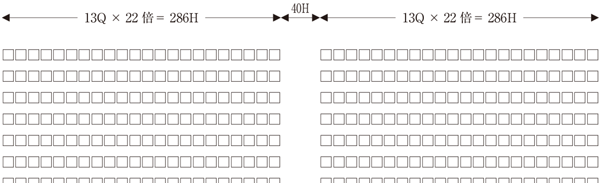
こういった計算が成り立ちます。実にシンプルです。
例2)13Q 字詰22倍 1H詰め 2段組 段間40Hの行長は、
[{ (13-1)×(22-1) }+13]×2+40=570
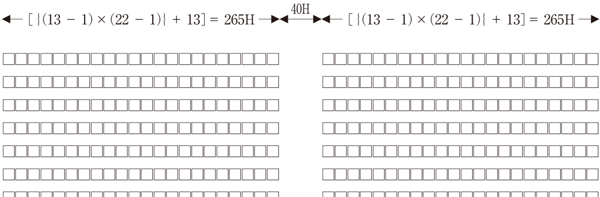
文字の送りを1歯詰めるだけで、計算が一気にここまで複雑に!
例1)が13Qのベタ組なのに対して、例2)では文字間が1H詰まっています。したがって、字詰めに掛ける数値は(13-1)となり、最後の文字のみ13が加算されるため、字詰めとして掛ける数値は(22-1)となります。
かなり遠回りですが、例1)の計算式を例2)のように記述すると
[{ (13-0)×(22-1) }+13]×2+40=612
こんな感じです。
理屈として、行長に掛ける数値は文字の級数ではなく、文字間である。
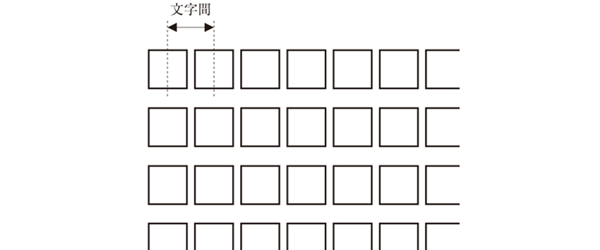
と、いうことです。
こういった具合に、行長のサイズを求めるだけでも、理論的な計算式が存在しています。
版面の行方向や1行アキ・半行アキなどの計算については、また別の機会に書きたいと思います。この計算が身に付くと指定を見ただけで、ある程度の形が頭に浮かぶようになってくるハズです。


